傻瓜也能看懂的机器学习教程【入门】

我一直批判很多教程，号称零基础，中间有很多东西衔接的时候有巨大的跨度，这篇文章也是记录自己在理解算法和神经网络的结果，标题可能有些夸张，但我相信我的读者都不是傻瓜。

线性回归

我们先来看一张图

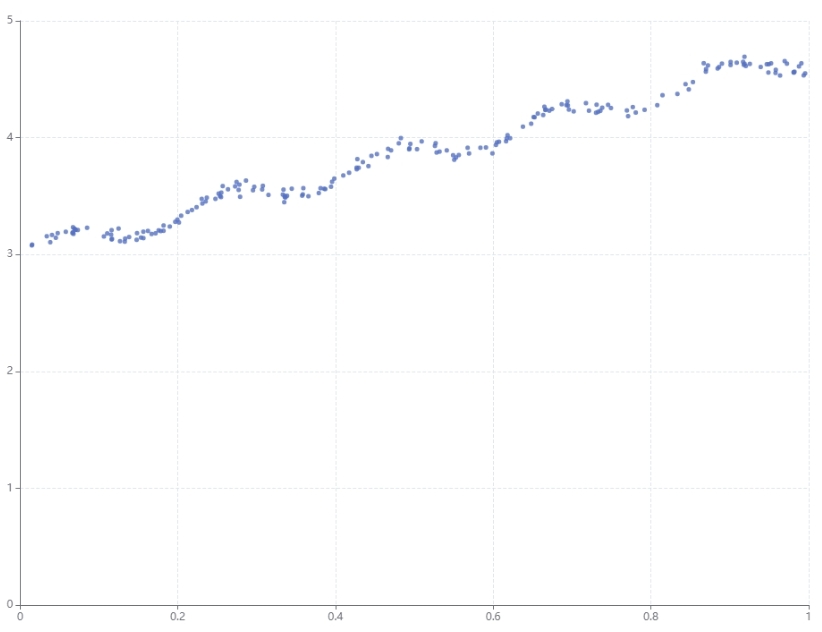
我们似乎能看到这些散点是有一个趋势的，但这个趋势应该怎么表达呢？没错，应该用一条线来表达，而线似乎可以是一个函数，那么我们就可以用函数来表达这个趋势，比如：$y = kx + b。$

其中 k 是斜率，b 是 y 轴的截距，那么我们就可以用这个函数来表达这个趋势，但是我们需要找到这个函数的参数 k 和 b，那么我们就需要一些数据来帮助我们找到这个函数的参数，这些数据就是我们的训练数据，我们需要用这些数据来训练我们的模型，使得我们的模型能够更好的表达这个趋势。

很多教程就开始用上面的语句来表达了，但我觉得还不够傻瓜直白，比如为什么是 y = kx + b，答案是，直线的表达方式就是这样，一条直线上所有的点的关系就是这个公式，其中x、y代表这个点的坐标，好了，那为什么是直线呢？这些散点明显看起来不是直线，对的没错，他看起来更近似于折线，不过因为我们在一个入门的教程，所以就先将其看作一个直线，因为这些点对然呈现出一条折现来，但它整体的趋势是一条直线，准确来说，这些点是单调变化的，单调变化的点都可以用线性回归来表示，而 y = kx + b 就是线性回归的表达方式，有点啰嗦哈。

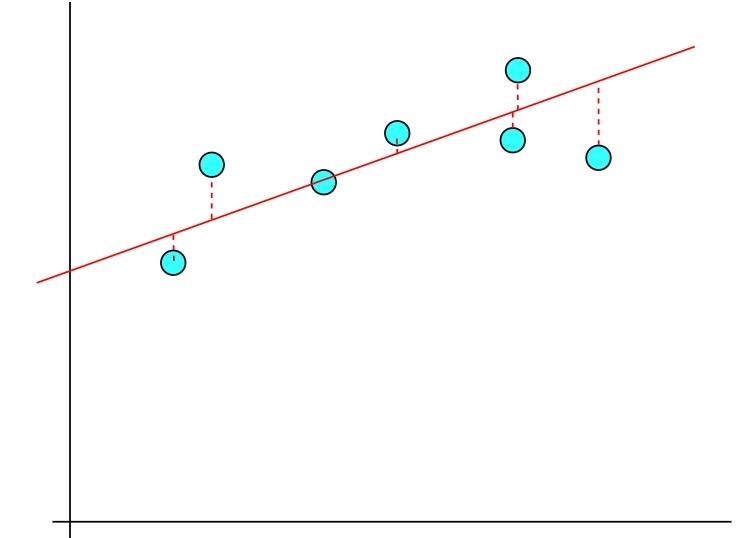
那么其中的关键就是计算 k 和 b 的值，从图上看，我们似乎要调整k,b的取值，来计算这些点到这条直线的所有距离，并且是最优距离（最贴近所有的点），抽象一下，也就是这些点到直线的距离（误差）的总和最小（当然没有最小了，只有尽量小），就是我们随便给k和b来取值，然后计算这些点到直线的距离，然后取这些距离的总和最小的 k 和 b ，这就是我们的目标，当然我们不是每次都胡乱赋值的，这个寻找下一个系数的过程叫做梯度下降，什么是梯度下降呢？

假设你站在一个山顶上，天很黑，你的任务是找到山谷最低的地方。但是，因为光线不好，你看不清楚远处的地形，只能靠周围的坡度来判断怎么走。梯度下降就像是你在下山的过程，每一步都沿着坡度最陡的方向往下走，一步一步地接近谷底，如果走每一步走的太小那下山就太慢了。

这看起来都是非常模糊的东西，我们的整个过程都需要转换成可重复性的工作才能交给计算机，而计算机的运算一定有一个初值、计算规则、结果校验。

那如例子所示，这里有几个问题：

1. 我现在在什么位置？
2. 我一步走多远？
3. 我应该往哪里走？

解决了上面这几个问题才能让计算机知道怎么走，然后让计算机知道什么时候停下来，也就是计算机帮我们在探路。

关于第一个问题也就是初始值怎么给，这里有好几种办法比如随便给一个值，比如 k = 0, b = 0，也可以把所有y的值的平均值设为初始的 b（因为 b 与 y 的关系更密切），然后 k = 0，说明这条直线没有斜率，这个初始值根据实际情况选择。

第二个问题，一步走多远？也就是调整 k 和 b每次的变化大小是多少，可以是0.01也可以是0.001，这个数字取决了我们的精度，如果设置过大，就会导致再最后计算阶段，多以步数值偏大，小一步数值过小，影响收敛。但数值过小，计算时常会增加。

最关键的就是第三个问题“我们应该往哪走？”，当然是距离之和最小的地方走，就是改变参数，然后挨个计算距离之和，看看还能不能更小，这个过程有一个公式均方误差公式：

$$MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - (kx_i + b))^2$$

• $y_i$ 是实际值；
• $kx_i + b$ 是预测值（我们拟合的直线上的值）；
• $n$ 是数据点的数量。

因为有的点在直线上方，有的在下方，直接相减后有正有负。平方让误差都变成正数，确保我们真正计算的是“距离”。另外平方还会放大较大的误差，这样在训练时会更关注偏离较大的点，让拟合的直线更加精准。

好了，这些交给计算机，他就可以开始找最优结了。

我写了这么多来说明这个问题可能很多人会觉得，最小二乘法 不是可以直接解决问题吗？~~~~请看文章标题，这里不解释了。

实际当中不会只有线性回归这一种，还有多项式回归、指数回归等等，上面仅仅描述一种使用计算机来求解某种边界问题的方法，旨在理解机器学习的基本原理，接下来介绍机器学习的一个重要应用，图像识别。

图像识别

我试图用最简单的方法来描述电脑是如何识别一个图片里含有人脸。上面已经描述了电脑是如何找到众多点的，线性回归线的，那么现在看下面的图：

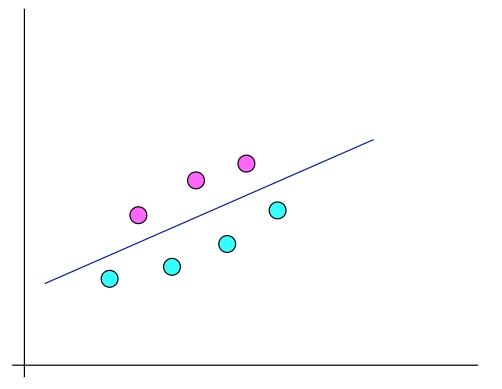
这条用于分割红色和青色的直线该怎么找到呢？回顾上一章节的方法和看图，我们可以判断这条直线必须是在青色点上方，也就是青色点的 y 值永远小于直线的 y 值，也就是 $y_i ≤ kx + b$ 而红色点相反 $y_i ≥ kx + b$，看图，发现这条直线的 k 、 b取值区间很大，很多直线符合这个要求，所以不难得出当点越多时，我们的直线描述的越准确，但现实中往往会出现下面这样的情况：

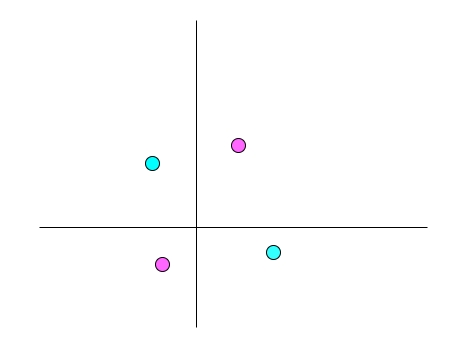
这又该如何表示呢？你会发现无论如何都没法用直线将两种颜色的点区分开，聪明的你肯定想到我是否可以将 y 值小于 0 的点的 x 值取反，然后再用直线来区分，这样就可以了。

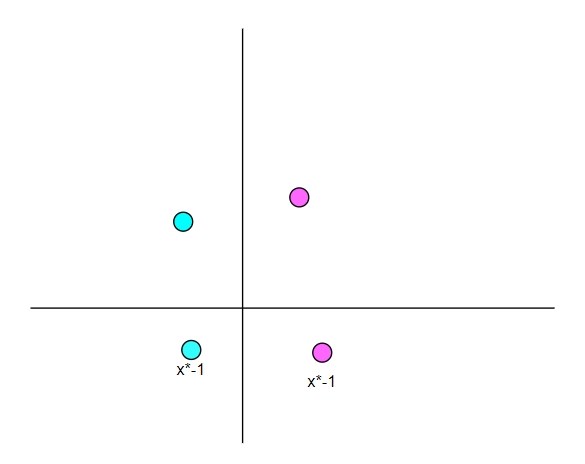
可是实际当中这有什么用呢？来看下面的图片：

计算机提取人脸特征点？但是计算机是怎么知道人脸的特征点的呢？首先需要对原始图片进行处理，怎么处理呢？就像上面最简单那个例子对像素点取反一样，可以将图形先进行处理，过程如下所示：

这里用到了一个叫 opencv的库 来进行处理，比如将 rgb（三原色）颜色的照片处理成灰度图，再用一些算法将其处理成比较好区分边界的数据，然后提取出这些点的数据信息，但是怎么样才能知道它的边界在哪里呢？看下面的图：

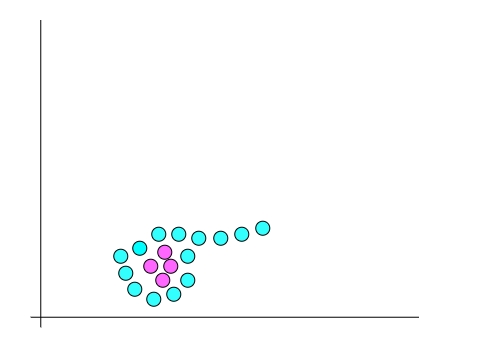
上图很容易就能明白，青色点就是边界，但为什么青色点是边界呢？因为他外面再没有点了，对于这种点就标记为边界点，然后让计算机再挨个扫描其相邻点，就像围棋找气孔一样。一般情况下像人脸识别我们用找边界的办法，知道眼睛、鼻子、嘴巴等位置、尺寸比例、在脸上的角度，然后人工标记出来。

一开始要形成这样的模型，我们就需要告诉计算机什么是眼睛、鼻子...，比如由人工框选了眼睛并定义图片为“眼睛”，然后计算机经过如上面描述的计算，将一张张照片的眼睛边界像素全部提取出来，这样的点越多，轮廓的边界线越收敛，这就形成了识别眼睛的数学公式。所以我们需要大量被标记的照片给计算机去处理，这个过程就是人工标注和训练。一个新的问题，这样的轮廓曲线的公式如何被记录呢？

一般来说我们使用一个叫傅里叶变换的算法来描述和比对轮廓，当然还有一些其他办法（比如 Hu 矩、HOG 等），这里仅说明傅里叶变换像素矩阵来比对记录轮廓，就类似一开始线性回归一样，找到用于描述这个轮廓的最优 k 和 b，当然，实际原理远比这复杂一些。

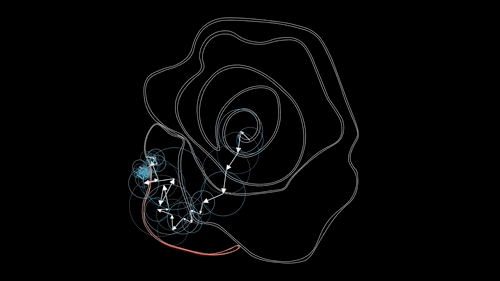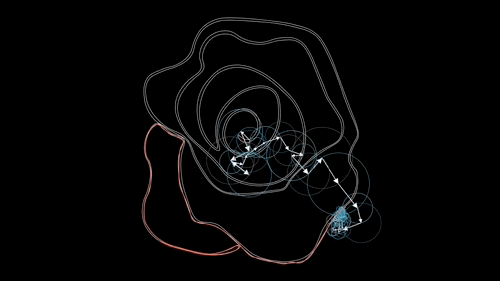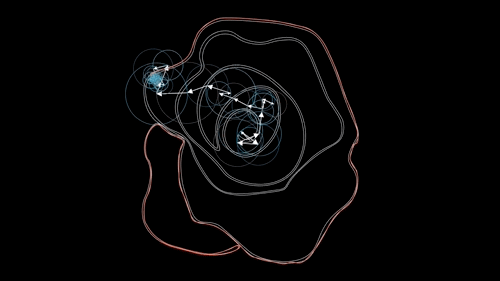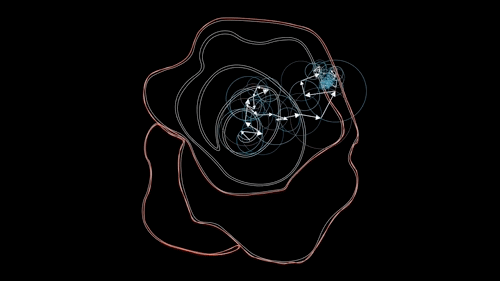
如图所示，一个叫傅里叶的人发现任何一个内部不存在交叉点、仅由一根完整的封闭曲线所组成的图形，那么我们可以将其同样看作为一个周期函数，从而用一个特定的傅里叶级数给表示出来，也就是我们可以将一系列边界点的连线，用一系列公式来表达，然后再将待比对的点带入这个公式以判断其相似度，就可以实现相应的识别功能了。

讲的比较粗浅，实际当中可能不只是将像素灰度处理，还要区分颜色点，还有不同光线等等，大部分过程我们都在处理不同环境下的照片，以便输入给算法的都能够正确处理，这些图像处理过程，包括轮廓比对 opencv 一般都能搞定，当然除了图像识别还有声音识别、文字识别等等，最麻烦的莫过于语义识别，特别是中文语义识别，用到的算法也不仅仅是上述，还有比较重要的如决策树、贝叶斯、随机森林等等都被分别用于预测、筛选、数据处理等。

本文旨在描述机器学习的基本原理，实际生产当中，有更多的难题需要解决，比如使用图像识别去辨识裂缝、运动距离，还需要根据相机焦距、像素比例、抖动等去做其他的计算，另外重要的神经网络本文没有着重描述，但大体上机器学习的思路就是如此，我们需要将现实当中的事物抽象成数学模型，把简单的重复性工作交给计算机去做，就如 【麻烦教育】 讲的，很多看似困难的事情其实并不困难，而是麻烦，而麻烦的事情交给机器就可以了，关键的问题是你得知道哪些东西可以交给机器和怎样交给机器。